本篇参考An Introduction to different Types of Convolutions in Deep Learning 介绍一下深度学习中不同的卷积操作。

卷积（Convolutions）

常规卷积操作如下动图所示，下方（浅蓝色矩形）为输入图像或特征图（feature map），阴影矩形（ $3 \times 3$ ）为卷积核，上方为输出的特征图。下方虚线边缘矩形为填充，为了在特定卷积核大小和步长下，得到合适的特征图。

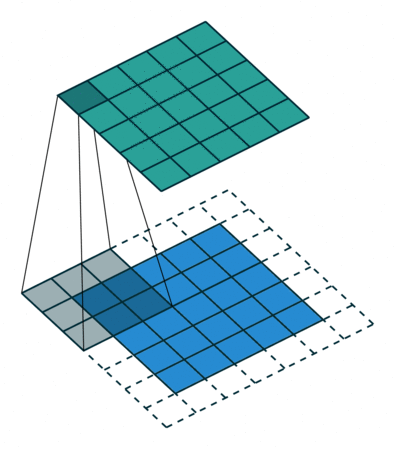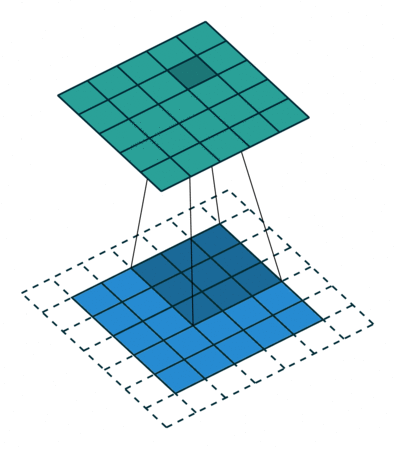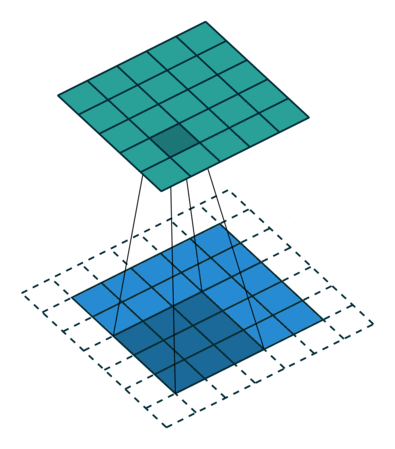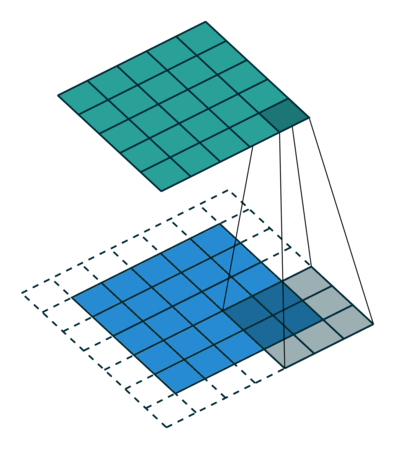
这里需要先介绍几个概念。

卷积核（kernel）

卷积核（卷积核包含至少一个 filter，有时也称 filter 为卷积核）中每个 filter 的大小决定了卷积操作的感受野。如上图所示，卷积核（也是filter，这里输出是单通道）是移动的阴影部分，大小为3，即 $3 \times 3$ 像素。对于输入图像，如果是RGB三通道，那么 filter 也应该是三通道的。如果想输出多通道，可设置多个 filter。即 filter 的通道数和输入图像一样，输出通道由卷积核的个数（filter 的个数）决定。

卷积核的大小一般设置成奇数，如 $1 \times 1, 3 \times 3, 5 \times 5, 7 \times 7$ 等，这是因为如下两点考虑：

更容易 padding. 常常想要保持卷积后图像尺寸不变，假设图像大小为 $n \times n$ ，卷积核大小为 $k \times k$ ，当 padding 的幅度设为 $(k - 1) / 2$ 时，步幅为1，卷积输出为 $(n - k + 2 \times ((k - 1) / 2)) / 1 + 1 = n$ . 但是，如果 $k$ 是偶数时，padding 的幅度就不能设置为 $(k - 1) / 2$ ，因为它不再是整数，无法实现；
更容易找到锚点。卷积时一般选择卷积核的某个位置为基准进行移动，通常选择卷积核的中心，如果卷积核大小为偶数，则无法找到锚点。

卷积输出图像尺寸的计算公式：

假设输入图像为 $n \times n$ ，卷积核大小为 $k \times k$ ，填充为 $p$ ，步幅为 $s$ ，那么输入图像大小为

⌊ \frac{n + 2 p - k}{s} ⌋ + 1

步幅（stride）

步幅决定了卷积核在图像上一次跨越的像素个数。如上图所示，卷积核在图像上一次平移一个像素。步幅常设为1，当设置更大步长时，类似于对图像进行下采样（如MaxPooling），即进行信息压缩，使得输出图像尺寸小于输入图像。步幅值就是缩放的倍数，如果步长设为2，输出就是输入的1/2.

填充（Padding）

填充定义了如何处理图像的边界。常用方法有两种，分别是 ‘same’ 和 ‘valid’:

same padding: 进行填充（通常填充0），允许卷积核超出原始图像边界，并使得卷积后的特征图与原来一致；
valid padding: 不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界。

输入输出通道

输入通道数决定了卷积核中每个 filter 的通道数，如输入通道数为 3，类似于 RGB 彩色图像。输出通道数决定了卷积核中有多少个 filter，如输出通道为 5，假设每个 filter 的尺寸为 $7 \times 7$ ，那么该卷积层需要的训练学习的参数个数为 $3 \times 7 \times 7 \times 5 = 735$ .

膨胀卷积（Dilated Convolutions）

膨胀卷积（a.k.a, also known as, atrous convolutions, 圆卷积），膨胀卷积为卷积层引入了另一个参数，称为膨胀率。这定义了卷积核中的值之间的间隔。膨胀率为 2 的 $3 \times 3$ 卷积核与 $5 \times 5$ 卷积核具有相同的视野，而仅使用 9 个参数。

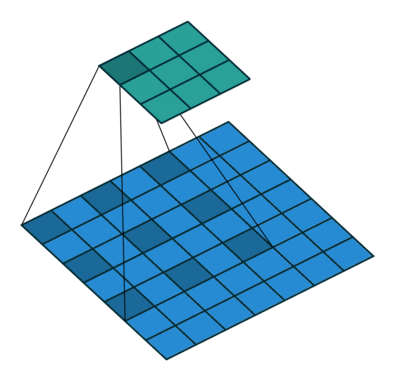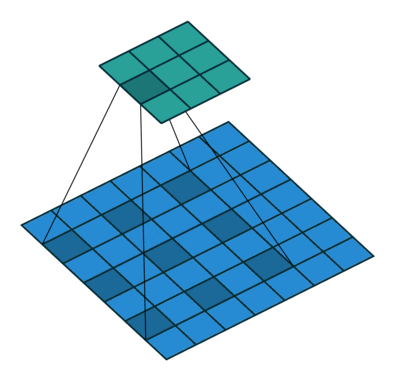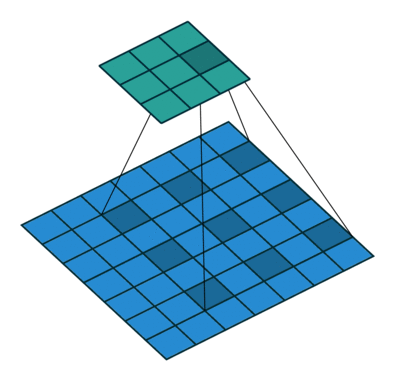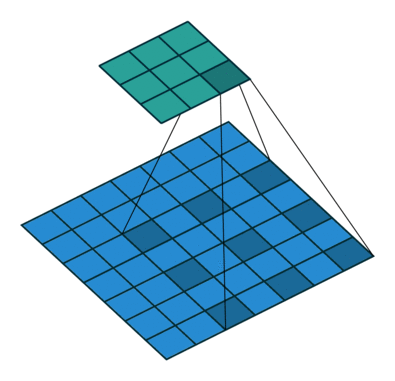
这以相同的计算成本提供了更广阔的视野。膨胀卷积在实时分割领域中特别流行。如果您需要广阔的视野并且无法承受多次卷积或更大的卷积核，请使用它们。

转置卷积（Transposed Convolutions）

转置卷积（a.k.a. deconvolutions or fractionally strided convolutions，又称为反卷积或分数步卷积）。有些文献使用反卷积名称，这是不合适的，因为它不是反卷积。更糟糕的是，确实存在反卷积，但在深度学习领域并不常见。实际的反卷积可还原卷积的过程。想象一下将图像输入到单个卷积层中。现在获取输出，将其放入黑盒，然后再次输出原始图像。这个黑匣子进行去卷积。它是卷积层功能的数学逆运算。

转置卷积有些类似，因为它产生的空间分辨率与假设的反卷积层相同。但是，对值执行的实际数学运算是不同的。转置的卷积层执行常规卷积，但还原其空间变换。

我们看一个具体的例子。 $5 \times 5$ 的图像被输入到卷积层。步幅设置为 2，禁用填充，卷积核尺寸为 $3 \times 3$ ，这将产生 $2 \times 2$ 的图像。

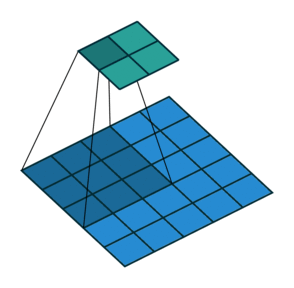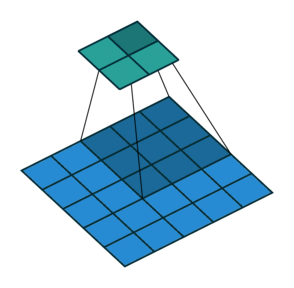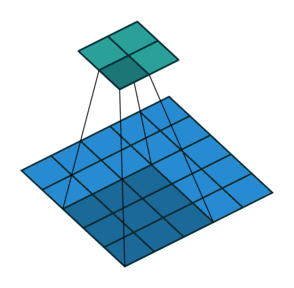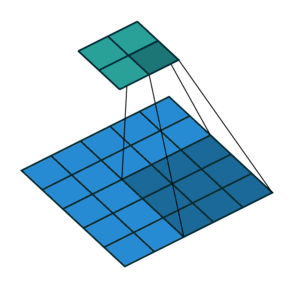
如果我们想逆转此过程，则需要进行逆数学运算，以便从我们输入的每个像素中生成 9 个值。然后，我们以 2 的步幅遍历输出图像。这将是反卷积。

转置卷积不会这样做。唯一的共同点是它可以确保输出也将是 $5 \times 5$ 的图像，同时仍执行正常的卷积操作。为了实现这一点，我们需要对输入执行一些华丽的填充。

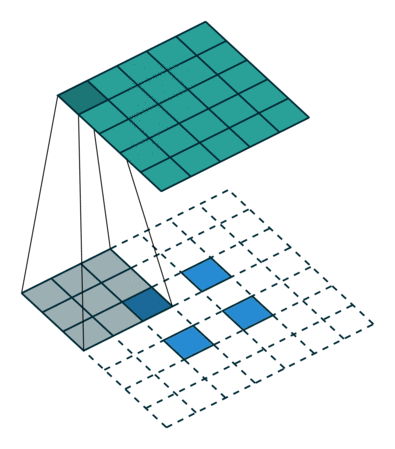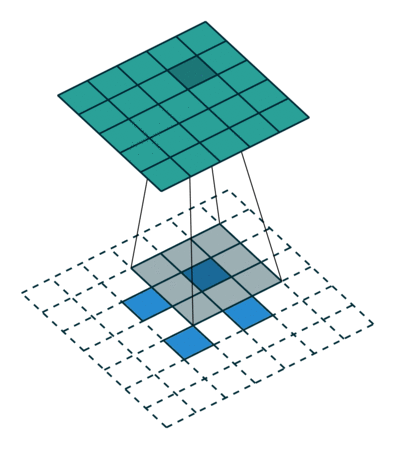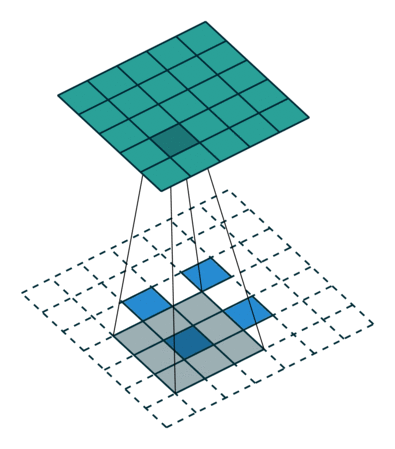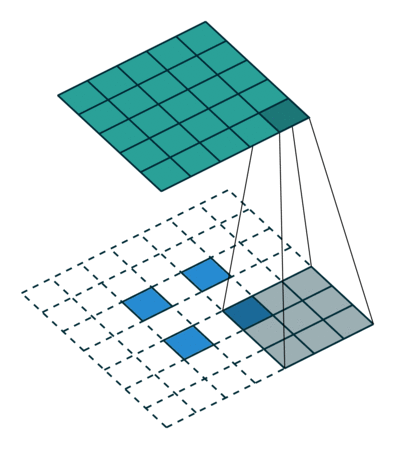
就像您现在可以想象的那样，此步骤不会从上面逆转该过程。至少不涉及数学逆操作。它仅从以前重建空间分辨率并执行卷积。这可能不是数学上的逆运算，但是对于 Encoder-Decoder 架构，它仍然非常有帮助。这样，我们可以将图像的放大与卷积结合在一起，而不必执行两个单独的过程。

可分离卷积（Separable Convolutions）

在可分离卷积中，我们能够把卷积操作分成多步进行。假设卷积表示为 $y = c o n v (x, k)$ ，其中 $y$ 为输出图像， $x$ 为输入图像， $k$ 为卷积核。并假设卷积核可以通过 $k = k_{1} . d o t (k_{2})$ 计算。这样可以进行可分离卷积，在 2D 上进行 $k$ 卷积等价于作两个 1D 的卷积 $k_{1}, k_{2}$ .

以图像处理中常常使用的 Sobel 卷积核为例，可以通过将向量 $[1, 0, - 1]$ 和 $[1, 2, 1]^{T}$ 相乘得到，在相同操作下，它只需要 6 个参数，而不是 9 个参数。

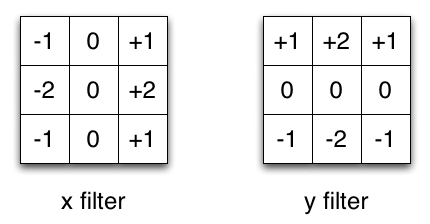
这种卷积操作称为空间可分离卷积。

但在深度学习中，深度可分离卷积常会遇到。假设输入图像是 16 通道，卷积核尺寸是 $3 \times 3$ ，输出通道是 32，按照上面的计算方法常规的卷积操作共有 $16 \times 3 \times 3 \times 32 = 4608$ 个参数。但是，如果进行深度可分离卷积，首先 16 个通道每一个经过 $3 \times 3$ 卷积，得到 16 个特征图，然后，再进行 32（得到 32 通道）个 $1 \times 1$ （每一个都是 16 通道）的卷积，整个过程一共需要 $16 \times 3 \times 3 + 16 \times 1 \times 1 \times 32 = 656$ 个参数。这里设置的深度乘子是 1.