Canny 图像边缘检测算法
图像边缘检测(Edge Detection)作为图像处理和计算机数据的基本问题,其目的是识别数字图像中亮度变化明显的点。图像中这些显著变化的部分反映了重要事件或其他变化,包括深度上的不连续,表面方向的不连续,物质属性的改变和场景照明的变化等。图像边缘检测能够剔除认为不相关的信息,大幅度地减少数据量,同时保留图像重要的结构属性。有两类边缘检测方法,一类是基于查找(一阶),一类是基于零穿越(二阶)。(根本上基于数学分析中方法,查找方法是寻求梯度最大的点,零穿越是寻求拐点,即二阶导数为 0 的点)基于查找的方法通过寻找图像一阶导数中的最大和最小值来检测边界,通常是将边界定位在梯度最大的方向。基于零穿越的方法通过寻找图像二阶导数零穿越来寻找边界,通常是 Laplacian 过零点或者非线性差分表示的过零点。
常用的边缘检测算子有:
- 一阶:Roberts Cross 算子, Prewitt 算子, Sobel 算子, Canny 算子,罗盘算子
- 二阶:Marr-Hildreth, 在梯度方向的二阶导数过零点。
Canny算子是最常用的边缘检测方法,图像边缘检测效果相对较优。
本篇主要介绍 Canny 图像边缘检测方法,因其作用的对象是数字图像,所以会简短介绍什么是数字图像处理、常见的数字图像分类、常用的边缘检测算子,最后重点介绍 Canny 边缘检测。
数字图像处理
数字图像处理(Digital Image Processing)是使用计算机处理图像成为更易于人类理解或需要的形式。常见的有,改善图示信息以便人类解释,优化图像存储、传输、表示,以便机器自动理解。具体的包括,人脸识别、车牌识别、图像边缘检测、图像目标分割、图像语义分割、视频目标跟踪等。
数字图像分类
数字图像是在计算机中以二维矩阵表示,每个元素都是数字像素灰度值,范围一般是 0 ~ 255. 常见的数字图像有二值图像、灰度图像、彩色图像等。
二值图像(Binary Image):每个像素的灰度值仅取 0 或 1,即分别是黑和白,因此可以理解为黑白图像。
灰度图像(Gray Scale Image):每个像素的灰度值取值于 0 ~ 255,0 表示纯黑,255 表示纯白,其他值表示由黑到白的渐变色。
彩色图像(Color Image):同灰度图像,但是是有三幅灰度图像层叠在一起组成,分别表示红(R)、绿(G)、蓝(B)三通道。
把彩色图像转化为灰度图像可以通过只选择三通道中的一个,也可以通过三通道对应位置进行加权平均计算得到,常用的加权系数有:
- G = 0.299 R + 0.587 G + 0.114 B
- G = 0.2126 R + 0.7152 G + 0.0722 B
- G = 0.2627 R + 0.6780 G + 0.0593 B
这些系数大多是基于人类对三种基准色的感官接收能力而定的。
像素邻域
既然数字图像是有像素(矩阵中的数值)组成,那么类似于矩阵,每个元素都有邻域元素,因此,数字图像像素也有像素邻域。常使用的邻域有:4 邻域、D 邻域和 8 邻域。
4 邻域:某个像素的上、下、左、右最邻近的像素点组成的 4 个像素集合;
D 邻域:某个像素的左上、左下、右上、右下最邻近的像素点组成的 4 个像素集合;
8 邻域:某个像素的 4 邻域和 D 邻域组成的 8 个像素集合;
图像滤波
常指的图像滤波是在保留图像细节特征的条件下对目标图像噪声进行抑制,作为图像预处理不可缺少的操作,结果直接影响后续图像处理和分析的有效性和可靠性。
当把数字图像的某一行取出后,其可以看作一个时间序列或波,同样,整幅图像也可以看作一种波,图像中亮度突变的部分就是高频部分,平滑的部分就是低频部分。对图像进行低通滤波就是使图像变得更平滑,滤除突变部分(包括噪声),图像变得模糊;对图像进行高通滤波就是提取图像的高频部分,只保留那些变化最快速最剧烈的区域,如边缘检测。
可通过在线网址进行图像滤波演示。浏览器实现滤波的范例代码,可以看这个仓库。
因此,广义的图像滤波不仅指消除图像噪声,还指通过滤波进行图像特征提取,简化图像信息,便于后续图像处理。
数字图像是二维数字矩阵,常用的滤波器(filter)也是一个二维数字矩阵,一般常取 $3\times 3$ 或 $5 \times 5$,奇数是为了保证中心点唯一,此时滤波器的半径分别是 1 和 2. 如深度学习中卷积神经网络中的卷积核就是一种滤波器,但是,其取值是通过大量图像数据经过反向传播学习得到的。本节介绍的边缘检测中使用的滤波器的每一个元素值是固定的,根据人们研究推断出来的。由此可看出,深度学习依据大数据学习得到合适的滤波器(模型参数),而传统的数字图像处理依据经验选择的滤波器。
边缘检测和常用滤波器
边缘检测是一种提取图像高频信息的过程,因此是一种图像高通滤波算法。如何得到滤波器呢?
梯度
既然边缘检测是提取高频部分,那么就需要通过一种手段描述高频部分,然后提取。把图像的某一行单独拿出来可以看作是一个函数曲线在自然数点上的采样,高频部分对应着导数绝对值比较大的部分。具体到图像上,就是使用差分近似导数。因为数字图像是二维的,所以有两个方向的导数,分别是 $x,y$,坐标原点是图像左上角,向下为 $y$ 轴,向右为 $x$ 轴。某一点的高频信息就使用该点在 $x,y$ 方向上的梯度来表示,梯度的模或大小是 $x,y$ 两方向导数的平方和再取平方根。梯度的方向是于 $x$ 轴的夹角。数学公式如下
假设某像素点 $P(x,y)$ 在 $x,y$ 方向的导数(差分)是
$$
d_x, d_y
$$
那么该点的梯度大小是
$$
G(x,y) = \sqrt{d_x^2 + d_y^2}
$$
梯度的方向是
$$
\theta = \arctan(\frac{d_y}{d_x})
$$
那么如何计算某像素点处导数或差分呢?常采用该像素 4 邻域或 8 邻域来计算得到,系数值组成滤波器,如下面的
Roberts 算子
$$
s_x =
\left [
\begin{matrix}
1 & 0 \\
0 & -1
\end{matrix}
\right],
s_y =
\left[
\begin{matrix}
0 & -1 \\
1 & 0
\end{matrix}
\right]
$$
Prewitt 算子
$$
s_x =
\left[
\begin{matrix}
-1 & 0 & 1 \\
-1 & 0 & 1 \\
-1 & 0 & 1
\end{matrix}
\right],
s_y =
\left[
\begin{matrix}
1 & 1 & 1 \\
0 & 0 & 0 \\
-1 & -1 & -1
\end{matrix}
\right]
$$
Sobel 算子
$$
s_x =
\left[
\begin{matrix}
1 & 0 & -1 \\
2 & 0 & -2 \\
1 & 0 & -1
\end{matrix}
\right],
s_y =
\left[
\begin{matrix}
1 & 2 & 1 \\
0 & 0 & 0 \\
-1 & -2 & -1
\end{matrix}
\right]
$$
使用检测算子对图像进行滤波的方法类似卷积神经网络,对于每一个像素,将滤波器矩阵的中心对应图像像素点,依次计算对应位置的矩阵元素乘积,然后将结果加到一起,得到该像素的滤波值。特别的对于边界点,超出边界部分填报 0. 计算后的图像和原图像同尺寸。
Sobel 算子 $s_x$ 表示检测 $x$ 轴方向边缘,计算得到 $x$ 轴方向的梯度,注意此时的边界方向应是垂直于 $x$ 轴,即 $y$ 轴,即梯度方向与边界方向垂直。
同理,Sobel 算子 $s_x$ 表示检测 $y$ 轴方向边缘,计算得到 $y$ 轴方向的梯度,注意此时的边界方向应是垂直于 $y$ 轴,即 $x$ 轴,即梯度方向与边界方向垂直。
注意,当计算的梯度值超出范围 $[0, 255]$ 时,常采用取绝对值。
同时,可以看到,简单的采用 Sobel 算子得到的梯度值图像(滤波后的图像)容易受噪声像素点的影响(可以考虑先滤波噪声,即低通滤波),也没有对结果进行后续处理,因为边缘信息可能很多不连续,断断续续比较多。
Canny 图像边缘检测
针对上述问题,1986年澳洲计算机科学家 John F. Canny 在文章 A Computational Approach to Edge Detection 中提出最优的边缘检测应该能够满足如下标准:
- 好的检测 - 算法能够尽可能多地标识出图像中的实际边缘;
- 好的定位 - 标识出的边缘要与实际图像中的实际边缘尽可能接近;
- 最小响应 - 图像中的边缘只能标识一次,并且可能存在的图像杂讯不应标识为边缘。
基于上面的三大标准,Canny 提出 5 步骤边缘检测算法,Canny 算子
- 首先利用高斯(低通)滤波器平滑图像,去除噪声;
- 其次利用 Sobel 算子计算像素梯度;
- 然后利用非最大抑制(Non-Maximum Suppression)消除边缘虚假信息,即“瘦边”;
- 再然后利用双阈值确定潜在边缘;
- 最后利用滞后(Hysteresis)跟踪边缘,即抑制弱边缘和未连接到强边缘的边缘。
Canny算子不容易受噪声干扰,得到的边缘精细且准确,缺点就是运算代价较高,运行于实时图像处理较困难,适用于高精度要求的应用
高斯低通滤波器 (Gaussian filter)
解决噪声影响
高斯滤波器也有称高斯模糊,是一种图像模糊滤波器,它用正态分布计算图像中每个像素的变换,二维空间中定义如下:
$$
G(x, y) = \frac{1}{2 \pi \sigma^2} e^{-(x^2 + y^2) / (2 \sigma^2)}
$$
离散化得到 $(2r + 1) \times (2r + 1)$ 的高斯核公式如下
$$
H_{ij} = \frac{1}{2 \pi \sigma^2} \exp(- \frac{(i - (r + 1))^2 + (j - (r + 1))^2}{2 \sigma^2}); 1\leq i, j \leq (2r + 1)
$$
常用的高斯核有,当$\sigma = 1, r = 2$ 时
$$
H_5 = \frac{1}{159}
\left[
\begin{matrix}
2 & 4 & 5 & 4 & 2 \\
4 & 9 & 12 & 9 & 4 \\
5 & 12 & 15 & 12 & 5 \\
4 & 9 & 12 & 9 & 4 \\
2 & 4 & 5 & 4 & 2
\end{matrix}
\right]
$$
图像梯度 (Finding the intensity gradient of the image)
找到边界点
经过高斯平滑后,能够消除噪声影响,再进行边缘检测将会容易些。通过 Sobel 算子计算图像上每个像素的梯度值和梯度方向。
非最大抑制 (Gradient magnitude thresholding or lower bound cut-off suppression)
解决边缘粗、宽
由上面可以,梯度方向是与 $x$ 轴的夹角,取值在 $[0, 360]$,Canny 将梯度方向依据 8 邻域分成 4 类,对角组成一类,因此每一类是 $360 / 4 = 90$ 度,每个角 45 度,如下图所示(图片引自知乎@程事在人)
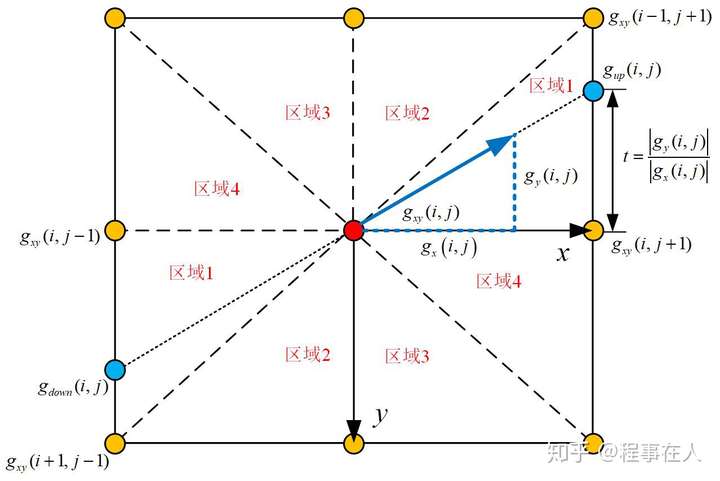
中心红点为当前像素位置 $(i, j)$,四面八方的黄点为 8 邻域像素位置,$x$ 轴上面划分为 1, 2, 3, 4 区域,下面也是,对角区域相同标识。假设当前像素点的梯度值是 $(g_x(i, j), g_y(i, j))$,梯度模或大小是 $g_{xy}(i, j)$,梯度方向指向上区域 1,负梯度方向指向下区域 1,对于上区域 1,计算上参照点 $g_{up}(i, j)$,比例因子是 $t = \frac{|g_y(i, j)|}{|g_x(i, j)|}$ ,如下计算
$$
g_{up}(i, j) = (1 - t) g_{xy}(i, j + 1) + t g_{xy}(i - 1, j + 1)
$$
类似的,计算下参照点 $g_{down}(i, j)$ 如下
$$
g_{down}(i, j) = (1 - t) g_{xy}(i, j - 1) + tg_{xy}(i + 1, j -1)
$$
然后,比较 $g_{xy}(i, j)$ 与 $g_{up}(i, j), g_{down}(i, j)$ 之间的大小,规则如下:
如果 $g_{xy}(i, j) \geq \max{g_{up}(i, j), g_{down}(i, j)}$ ,那么 $g_{xy}(i, j)$ 可能是边,否则,应该被抑制,令 $g_{xy}(i, j) = 0$. 注意,当 $g_x(i, j) = g_y(i, j) = 0$ 时,说明像素点不是边缘点。
双阈值 (Double threshold)
解决定位不准
上面三步已经能够大体给出边缘轮廓,但是,仍然存在一些伪边缘,当使用单一阈值截断时,容易导致边缘不连续。
当梯度值大于等于高阈值时,认为是强边缘;当梯度值小于低阈值时,认为是伪边缘,直接丢弃;对于大于等于低阈值,小于高阈值的边缘点,认为是弱边缘点,进行下一步处理。
滞后跟踪边缘 (Edge tracking by hysteresis)
解决间断点多
经过双阈值判定后,强阈值边缘作为真正的边缘,对于弱边缘还需要进一步的判断是否保留和丢弃。依据的规则是:
对于弱边缘像素,如果其 8 邻域像素中包含强边缘像素,则其为边缘点,否则不是,将赋值为 0,抑制。
强边缘像素肯定应该包含在最终边缘图像中,因为它们是从图像的真实边缘中提取的。但是,关于弱边缘像素会有一些争论,因为这些像素可以从真实边缘提取,也可以从噪声/颜色变化中提取。为了获得准确的结果,应消除由后一种原因引起的薄弱边缘。通常,在未连接噪声响应的情况下,由真实边缘引起的弱边缘像素将连接到强边缘像素。为了跟踪边缘连接,通过查看弱边缘像素及其 8 个连接的邻域像素来进行斑点分析。只要斑点中包含一个强边缘像素,该弱边缘点就可以被识别为应该保留的边缘点。
OpenCV 边缘检测
1 | import cv2 |





