本节介绍一些典型的聚类算法，如 K-Means，DBSCAN，谱聚类，层次聚类，optics，birch 等。聚类就是对大量未知标注的数据，按照内在相似性将其划分为多个类别，使类别内的数据相似度较大而类别间的数据相似度较小。通过计算每个类的代表点可以获得整个数据集的少量代表点，从而获得整个数据集的结构、形状信息。聚类算法通常处理无标签的数据集，因此常使用相似度或距离来处理。有衡量两个点（向量）之间的距离的，有衡量两个子集合之间的距离的，也有衡量点到子集合之间距离的。

首先先给出一个图，来直观看一下各个聚类算法的效果图。

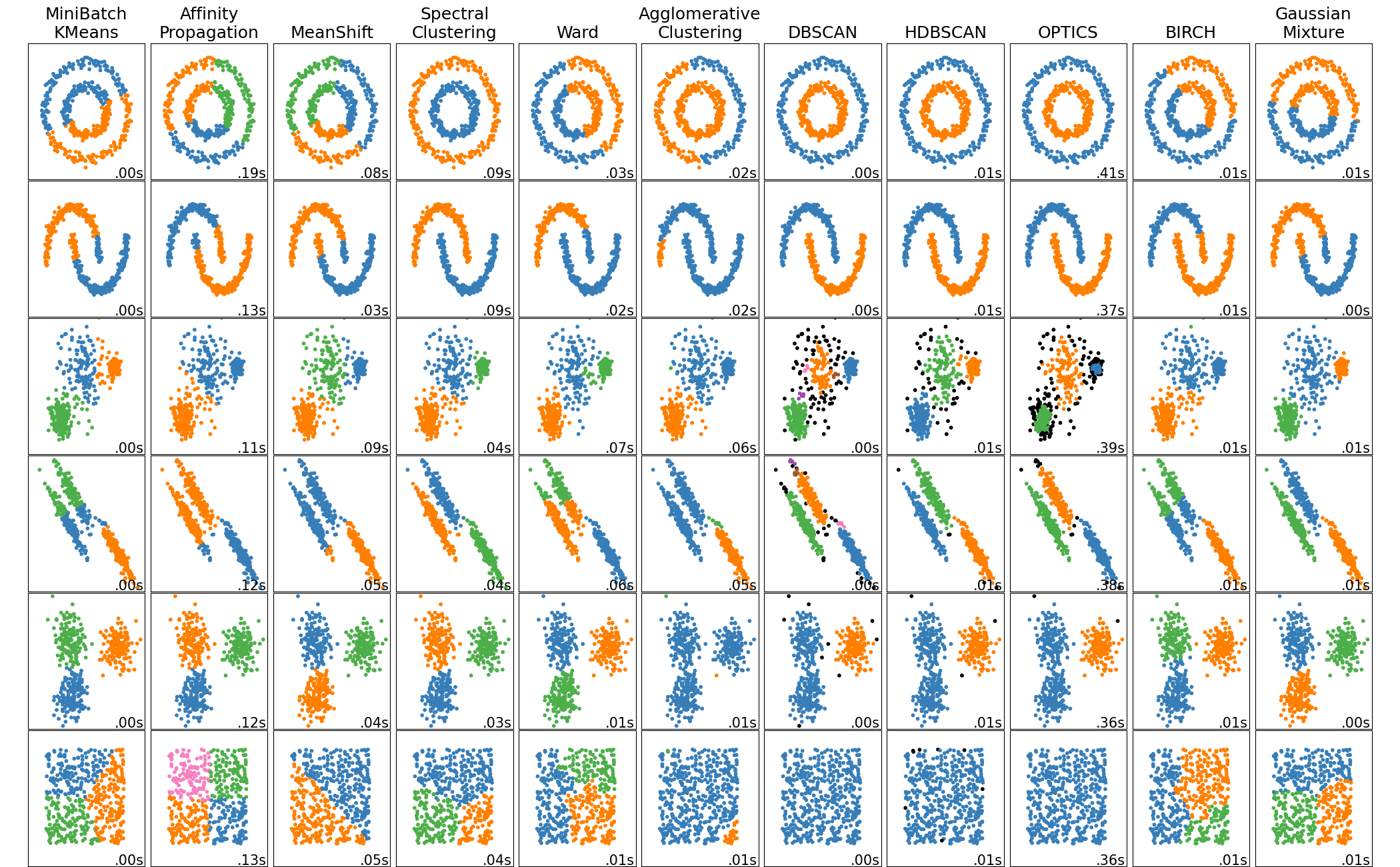
数学上，什么是距离？非空集合 $X$ 上的度量为一个函数（称之为“距离函数”或简称为“距离”）
$$
d: X \times X \to \mathbb{R}
$$
这里的 $\mathbb{R}$ 是实数集合，且对于所有 $X$ 内的 $x, y, z$，均满足如下条件：

非负性，或分离公理
$$
d(x, y) \geq 0
$$
同一性，或同时公理
$$
d(x,y) = 0 \Longleftrightarrow x = y
$$
对称性
$$
d(x, y) = d(y, x)
$$
次加性，或三角不等式
$$
d(x, z) \leq d(x, y) + d(y, z)
$$
其次，给出几种计算相似度或距离的方法。

闵可夫斯基（或叫明氏）距离（Minkowski，欧式空间中的一种距离，$p$-范数距离，$p$不一定要是整数，但不可以小于1，不然三角不等式不成立）
$$
d(\vec{x}, \vec{y}) = (\sum_{i=1}^n |x_i - y_i|^p)^{\frac{1}{p}}
$$
当 $p = 1$ 时，称为曼哈顿距离（Manhattan，1-范数距离），$p = 2$ 时，称为欧式（欧几里得）距离（Euclidean，2-范数距离），$p = +\infty$ 时称为切比雪夫距离（Chebyshev，无穷范数距离）。
杰卡德（Jaccard）相似系数
$$
J(A, B) = \frac{|A \cap B|}{|A \cup B|}
$$
余弦相似度（cosine similarity）
$$
cos(\theta) = \frac{\vec{x}^T \vec{y}}{|\vec{x}| \cdot |\vec{y}|}
$$
Pearson 相似系数
$$
\rho_{\vec{x}\vec{y}} = \frac{cov(\vec{x}, \vec{y})}{\sigma_{\vec{x}}\sigma_{\vec{y}}} = \frac{E[(\vec{x} - \mu_{\vec{x}})(\vec{y} - \mu_{\vec{y}})]}{\sigma_{\vec{x}}\sigma_{\vec{y}}}
$$
相对熵（K-L散度，K-L距离）
$$
D(p | q) = \sum_{\vec{x}} p(\vec{x}) \log{\frac{p(\vec{x})}{q(\vec{x})}} = E_{p(\vec{x})} \log{\frac{p(\vec{x})}{q(\vec{x})}}
$$
Hellinger 距离
$$
D_{\alpha}(p | q) = \frac{2}{1-\alpha^2}(1 - \int p(x)^{\frac{1+\alpha}{2}} q(x)^{\frac{1-\alpha}{2}} \mathrm{d}x)
$$

K-Means

k-means 算法是使用最多，且相对简单的聚类算法。

k-means 算法，也被称为 k-平均或k-均值，是一些聚类算法的基础，如谱聚类。

假设输入样本为 $S = x_1, x_2, \cdots, x_m$，则算法步骤为

选择初始的 $k$ 个类别中心 $\mu_1, \mu_2, \cdots, \mu_k$
对于每个样本 $x_i$，将其标记为距离类别中心最近的类别，即
$$
label_i = \underset{1 \leq j \leq k}{\arg \min} | x_j - \mu_j |
$$
将每个类别中心更新为隶属该类别的所有样本的均值
$$
\mu_j = \frac{1}{|c_j|} \underset{i \in c_j}{\sum} x_i
$$
重复最后两步，直到类别中心的变化小于某阈值。或者迭代次数达到某阈值，或者最小平方误差MSE（Minimum Squared Error）小于某阈值。

在算法中，如果不取均值，改为取中位数，称为 k-mediods 聚类（k中值聚类）。

初始值的选择对 k-means 算法影响很大，通过 k-means++ 可以有效的选择初始聚类中心。具体的，

首先任意选择一个初始样本点 $\mu_1 = x_1$ 为第一个聚类中心
其次，计算剩余点 $y_1, y_2, \cdots, y_m$ 到聚类中心 $\mu_1$ 的聚类，假设为 $d_1, d_2, \cdots, d_m$，那么依概率 $\frac{d_1}{d}, \frac{d_2}{d}, \cdots, \frac{d_m}{d}$ 来选择样本点 $y_1, y_2, \cdots, y_m$ 中的一个作为第二个聚类中心 $\mu_2$，其中 $d = \sum_{i=1}^m d_i$
重复步骤2，直到选到所需的 $k$ 个聚类中心 $\mu_1, \mu_2, \cdots, \mu_k$
最后，使用 k-means 聚类算法在数据集 $x_1, x_2, \cdots, x_n$ 和 $k$ 个聚类中心 $\mu_1, \mu_2, \cdots, \mu_k$ 上进行迭代聚类

关于簇数即聚类中心个数的选择，一种方法是遍历簇数取值 $1, 2, \cdots, n$，画图查看不同簇数取值下整个数据集 MSE 变化情况，即从数据集方差（当类簇数等于1）下降到0（当类簇数等于 $n$，即样本个数，每个样本聚成一个类），选择 MSE 变化的“肘关节点”；另一种方法是，当选择某个 $k$ 作为聚类中心树，进行 k-means 聚类，计算聚类后每个类簇的 MSE，对于取值较大 MSE 的类簇增加聚类中心个数，对于取值较小的，合并聚类中心。

k-means 深层解释

假设样本集 ${ x_i }$ 有 $k$ 个簇，每个簇样本数目为 $N_1, N_2, \cdots, N_k$，且每个簇都服从相同方差 $\sigma$ 的高斯分布，每个类簇的均值就是聚类中心 $\mu_i$，那么，k-means 聚类的最大似然函数是
$$
\Pi_{j=1}^k \Pi_{i=1}^{N_j} \frac{1}{\sqrt{2\pi}\sigma} \exp ^{-\frac{(x_i^{j} - \mu_j)}{2\sigma^2}}
$$
取对数后，只保留参数 $\mu_i$ 部分
$$
J(\mu_1, \mu_2, \cdots, \mu_k) = \frac{1}{2} \sum_{j=1}^k \sum_{i=1}^{N_j} (x_i^j - \mu_j)^2
$$
对函数 $J$ 关于参数变量 $\mu_1, \mu_2, \cdots, \mu_k$ 求偏导，得到
$$
\frac{\partial J}{\partial \mu_j} = - \sum_{i=1}^{N_j}(x_i^j - \mu_j) = 0 \Rightarrow \mu_j = \frac{1}{N_j} \sum_{i=1}^{N_j} x_i^j
$$
由此可以知道，k-means 运行的隐含假设是，每个类簇都服从高斯分布，且方差相同。即数据集服从方差相同的混合高斯分布。同时，该算法的目标函数是 MSE，且采用梯度下降算法进行迭代优化。因此，机器学习中非凸函数梯度下降算法的问题，该算法都会有，比如，初始点（初始聚类中心）的选择，局部最优问题，收敛震荡问题，鞍点问题等。同时，也提醒我们，可以使用 SGD 来求解 k-means（即 Mini-batch k-means 算法，不是把每个类的算有点个数 $N_j$ 都使用来计算均值，而是随机使用部分点 $N_j^{\prime} < N_j$ 来计算均值），同样的，也可以采用 k-means++ 筛选初始点的方法来选择机器学习方法初始点。

k-means 聚类算法的优缺点

优点：

是解决聚类问题的一种经典算法，简单，快速
对处理大数据集，该算法保持可伸缩性和高效率
当簇近似分为高斯分布时，效果较好
可作为其他聚类方法的基础，如谱聚类

缺点：

在簇的平均值可被定义的情况下才能使用，可能不适应于某些应用
必须事先给出 $k$ 值（要生成的簇个数），而且对初值敏感，对于不同的初始值，可能会导致不同结果
不适合于发现非凸形状的簇或者大小差别很大的簇
对噪声和孤立点数据敏感

KMeans 算法的重要参数包括：n_clusters.

python 代码示例：

import numpy as np
from sklearn.cluster import KMeans

X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
kmeans.labels_
# 聚类结果如下
array([1, 1, 1, 0, 0, 0], dtype=int32)

kmeans.cluster_centers_
# 聚类中心
array([[10.,  2.],
       [ 1.,  2.]])

也可以直接返回聚类结果，不显示调用 clustering.labels_

1
2
3

KMeans(n_clusters=2, random_state=0).fit_predict(X)
# 直接打印出来聚类结果
array([1, 1, 1, 0, 0, 0], dtype=int32)

MiniBatchKMeans 算法的重要参数包括：n_clusters, batch_size.

MiniBatchKMeans 一般会比 KMeans 结果差，但是运行更快。

python 代码示例：

import numpy as np
from sklearn.cluster import MiniBatchKMeans

X = np.array(
    [
        [1, 2],
        [1, 4],
        [1, 0],
        [4, 2],
        [4, 0],
        [4, 4],
        [4, 5],
        [0, 1],
        [2, 2],
        [3, 2],
        [5, 5],
        [1, -1],
    ]
)
kmeans = MiniBatchKMeans(n_clusters=2, random_state=0, batch_size=6, max_iter=10).fit(X)
kmeans.labels_
# 聚类结果如下
array([1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1], dtype=int32)

kmeans.cluster_centers_
# 聚类中心
array([[3.95918367, 2.40816327],
       [1.12195122, 1.3902439 ]])

也可以直接返回聚类结果，不显示调用 clustering.labels_

1
2
3

MiniBatchKMeans(n_clusters=2, random_state=0, batch_size=6, max_iter=10).fit_predict(X)
# 直接打印出来聚类结果
array([1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1], dtype=int32)

DBSCAN

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）算法是一种基于密度的聚类算法。密度聚类方法的指导思想是，只要样本点的密度大于某阈值，则将该样本添加到最近的簇中。这类算法能克服基于距离的算法只能发现“类圆形”（凸）的聚类的缺点，可发现任意形状的聚类，且对噪声数据不敏感。但计算密度单元的计算复杂度大，需要建立空间索引来降低计算量。

DBSCAN 是一个比较有代表性的基于密度的聚类算法。与下面将要介绍的层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在有“噪声”的数据中发现任意形状的聚类。

介绍 DBSCAN 需要了解如下几个概念：

对象的 $\varepsilon$-邻域：给定对象在半径 $\varepsilon$ 内的区域。
核心对象：对于给定的数目 $m$，如果一个对象的 $\varepsilon$-邻域至少包含 $m$ 个对象，则称该对象为核心对象。
直接密度可达：给定一个对象集合 $D$，如果 $p$ 是在 $q$ 的 $\varepsilon$-邻域内，而 $q$ 是一个核心对象，我们说对象 $p$ 从对象 $q$ 出发是直接密度可达的。
密度可达：如果存在一个对象链 $p_1, p_2, \cdots, p_n, p_1 = q, p_n = p$，对 $p_i \in D, (i \leq i \leq n)$, $p_{i+1}$ 是从 $p_i$ 关于 $\varepsilon$ 和 $m$ 直接密度可达的，则对象 $p$ 是从对象 $q$ 关于 $\varepsilon$ 和 $m$ 密度可达的。
密度相连：如果对象集合 $D$ 中存在一个对象 $o$，使得对象 $p$ 和 $q$ 是从 $o$ 关于 $\varepsilon$ 和 $m$ 密度可达的，那么对象 $p$ 和 $q$ 是关于 $\varepsilon$ 和 $m$ 密度相连的。
簇：一个基于密度的簇是最大的密度相连对象的集合。
噪声：不包含在任何簇中的对象称为噪声。

DBSCAN 算法流程：

如果一个点 $p$ 的 $\varepsilon$-邻域包含多于 $m$ 个对象，则创建一个 $p$ 作为核心对象的新簇；
寻找并合并核心对象直接密度可达的对象；
没有新点可以更新簇时，算法结束。

从算法流程可以看出，每个簇至少包含一个核心对象。非核心对象可以是簇的一部分，构成了簇的边缘。包含过少对象的簇被认为是噪声。DBSCAN 不需要事先给定聚类个数。对于大数据集因为要计算密度，不太适用。

DBSCAN 优势：

不需要指定簇的个数
可以发现任意形状的簇
擅长找到离群点（检测任务）
需要的参数较少

DBSCAN 劣势：

高纬数据处理比较困难（可以先降维）
参数难以选择（参数对结果的影响非常大）
scikit-learn 中效率很慢（使用数据消减策略）

DBSCAN 算法的重要参数包括：$\varepsilon$=eps, m=min_samples.

python 代码示例：

import numpy as np
from sklearn.cluster import DBSCAN

X = np.array([[1, 2], [2, 2], [2, 3], [8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)
clustering.labels_
# 聚类结果如下
array([ 0,  0,  0,  1,  1, -1])

也可以直接返回聚类结果，不显示调用 clustering.labels_

1
2
3

DBSCAN(eps=3, min_samples=2).fit_predict(X)
# 直接打印出来聚类结果
array([ 0,  0,  0,  1,  1, -1])

谱聚类

谱聚类通过计算矩阵的特征向量来实现。可以把谱聚类描述为 PCA + K-means.

谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的目的。可以解决区域重叠问题。

谱分析的整体过程：

给定一组数据 $x_1, x_2, \cdots, x_n$，记任意两个点之间的相似度（“距离” 的负函数）为 $s_{ij} = <x_i, x_j>$，形成相似度图：$G=(V, E)$. 如果 $x_i$ 和 $x_j$ 之间的相似度 $s_{ij}$ 大于一定的阈值，那么，两个点是连接的，权值记作 $s_{ij}$.
接下来，可以用相似度图来解决样本距离问题：找到图的一个划分，形成若干个组，使得不同组之间有较低的权值，组内有较高的权值。

谱聚类的流程：

计算任意两个样本之间的相似度，这里常采用高斯相似度 $w_{ij} = exp(-\frac{|x_i - x_j|^2}{2\sigma^2})$, 这里 $\sigma$ 是超参数；
构造相似度矩阵 $W = (w_{ij})$，需要注意的是，主对角线元素本来是 $w_{ii} = 1$，这里替换成 0；
构造度矩阵 $D = diag(d_i)$，这里 $d_i = \sum_{i=1}^n w_{ij}$;
构造拉普拉斯矩阵 $L = D - W$，如二维的例子对应的拉普拉斯矩阵如下

$$D = \begin{bmatrix}
w_{12} + w_{13} & 0 & 0 \\
0 & w_{21} + w_{23} & 0 \\
0 & 0 & w_{31} + w_{32}
\end{bmatrix}$$

$$W = \begin{bmatrix}
0 & w_{12} & w_{13} \\
w_{21} & 0 & w_{23} \\
w_{31} & w_{32} & 0
\end{bmatrix} $$

$$L = \begin{bmatrix}
w_{12} + w_{13} & -w_{12} & -w_{13} \\
-w_{21} & w_{21} + w_{23} & -w_{23} \\
-w_{31} & -w_{32} & w_{31} + w_{32}
\end{bmatrix}$$
求拉普拉斯矩阵的谱，即所有的特征向量，并从小到大进行排列，假设为 $\lambda_1, \lambda_2, \cdots, \lambda_k, \cdots, \lambda_n$, 其对应的特征向量分别为 $\mu_1, \mu_2, \cdots, \mu_k = (\mu_{ik})^T, \cdots, \mu_n$，其中，特征向量
$$
\begin{bmatrix}
\mu_{11} & \mu_{12} & \cdots & \mu_{1k} & \cdots & \mu_{1n} \\
\mu_{21} & \mu_{22} & \cdots & \mu_{2k} & \cdots & \mu_{2n} \\
\vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\
\mu_{n1} & \mu_{n2} & \cdots & \mu_{nk} & \cdots & \mu_{nn}
\end{bmatrix}
$$

的每一行就是样本映射的特征。选取前 $k$ 列个特征向量（前 $k$ 小特征值对应的特征向量）作为主特征向量（类似 PCA），然后，对矩阵
$$
\begin{bmatrix}
\mu_{11} & \mu_{12} & \cdots & \mu_{1k} \\
\mu_{21} & \mu_{22} & \cdots & \mu_{2k} \\
\vdots & \vdots & \ddots & \vdots \\
\mu_{n1} & \mu_{n2} & \cdots & \mu_{nk}
\end{bmatrix}
$$
按行聚类，采用聚类方法 k-means，这样就得到了原始样本的谱聚类。

证明，拉普拉斯矩阵 $L = D - W$ 是半正定矩阵。

对任意非零向量 $f$
$$
f^T L f = f^T D f - f^T W f = \sum_{i=1}^n d_i f_i^2 - \sum_{i,j=1}^n f_i f_j w_{ij} \\
= \frac{1}{2} (\sum_{i=1}^n d_i f_i^2 - 2 \sum_{i,j=1}^n f_i f_j w_{ij} + \sum_{j=1}^n d_j f_j^2) \\
= \frac{1}{2} \sum_{i,j=1}^n w_{ij}(f_i - f_j)^2 \geq 0.
$$
$L$ 是对称半正定矩阵，最小特征值是0，相应的特征向量是全1向量。其他特征值大于零。

它适用于少数群集，但不建议用于许多群集。

谱聚类算法：未正则拉普拉斯矩阵

输入：$n$ 个点 ${x_i}_{i=1, 2, \cdots, n}$，簇的数目 $k$

计算 $n \times n$ 的相似度矩阵 $W$ 和度矩阵 $D$
计算拉普拉斯矩阵 $L = D - W$
计算 $L$ 的前 $k$ 个特征向量 $\mu_1, \mu_2, \cdots, \mu_k$
将 $k$ 个列向量 $\mu_1, \mu_2, \cdots, \mu_k$ 组成矩阵 $U \in \mathbb{R}^{n \times k}$
对于 $i = 1, 2, \cdots, n$，令 $y_i \in \mathbb{R}^k$ 是 $U$ 的第 $i$ 行的向量
使用 k-means 算法将点 ${y_i}_{i=1, 2, \cdots, n}$ 聚类成簇 $C_1, C_2, \cdots, C_k$
输出簇 $A_1, A_2, \cdots, A_k$，其中，$A_i = {j|y_j \in C_i}$

谱聚类算法：随机游走拉普拉斯矩阵

输入：$n$ 个点 ${x_i}_{i=1, 2, \cdots, n}$，簇的数目 $k$

计算 $n \times n$ 的相似度矩阵 $W$ 和度矩阵 $D$
计算拉普拉斯矩阵 $L_{rw} = D^{-1}(D - W)$
计算 $L$ 的前 $k$ 个特征向量 $\mu_1, \mu_2, \cdots, \mu_k$
将 $k$ 个列向量 $\mu_1, \mu_2, \cdots, \mu_k$ 组成矩阵 $U \in \mathbb{R}^{n \times k}$
对于 $i = 1, 2, \cdots, n$，令 $y_i \in \mathbb{R}^k$ 是 $U$ 的第 $i$ 行的向量
使用 k-means 算法将点 ${y_i}_{i=1, 2, \cdots, n}$ 聚类成簇 $C_1, C_2, \cdots, C_k$
输出簇 $A_1, A_2, \cdots, A_k$，其中，$A_i = {j|y_j \in C_i}$

谱聚类算法：对称拉普拉斯矩阵

输入：$n$ 个点 ${x_i}_{i=1, 2, \cdots, n}$，簇的数目 $k$

计算 $n \times n$ 的相似度矩阵 $W$ 和度矩阵 $D$
计算拉普拉斯矩阵 $L_{sym} = D^{-1/2}(D - W)D^{-1/2}$
计算 $L$ 的前 $k$ 个特征向量 $\mu_1, \mu_2, \cdots, \mu_k$
将 $k$ 个列向量 $\mu_1, \mu_2, \cdots, \mu_k$ 组成矩阵 $U \in \mathbb{R}^{n \times k}$
对于 $i = 1, 2, \cdots, n$，令 $y_i \in \mathbb{R}^k$ 是 $U$ 的第 $i$ 行的向量
对于 $i=1,2,\cdots, n$，将$y_i \in \mathbb{R}^k $ 依次单位化，使得 $|y_i| = 1$
使用 k-means 算法将点 ${y_i}_{i=1, 2, \cdots, n}$ 聚类成簇 $C_1, C_2, \cdots, C_k$
输出簇 $A_1, A_2, \cdots, A_k$，其中，$A_i = {j|y_j \in C_i}$

有时候，也会使用拉普拉斯矩阵 $L = W - D$，或者 $L = D^{-1}W$ (因为 $L = D^{-1}(D-W) = I - D^{-1}W$，不考虑单位矩阵效果一样)，此时，需要对特征值进行从大到小排列，选取相应的特征向量。

当未给定先验知识的情况下，优先选择随机游走拉普拉斯矩阵。对于 $n$ 个样本，通过相似度构建一个相似度连通图，共有 $n(n+1)/2$ 条边，边上的权重就是两个样本之间的相似度。那么谱聚类的目标函数就是使用剪刀剪断一个边使得损失值最小（即特征值）。

随机游走和拉普拉斯矩阵的关系（当拉普拉斯矩阵 $L = D^{-1}W$ 时）

图论中的随机游走是一个随机过程，它从一个顶点跳转到另外一个顶点。谱聚类即找到图的一个划分，使得随机游走在相同的簇中停留而几乎不会游走到其他簇。转移矩阵是 $P=D^{-1}W$，表示从顶点 $v_i$ 跳转到顶点 $v_j$ 的概率正比于边的权值，即 $p_{ij} = w_{ij}/d_i$.

进一步的，可以考虑：

谱聚类中的 $k$ 如何确定？$k^{\star} = \arg \max_k |\lambda_{k+1} - \lambda_k|$
最后一步的 $k-means$ 的作用是什么？目标函数是关于子图划分指示向量的函数，该向量的值根据子图划分确定，是离散的。该问题是 NP 的，转化成求连续实数域上的解，最后用 $k-means$ 算法离散化
未正则、对称、随机游走拉普拉斯矩阵，首先哪个？随机游走拉普拉斯矩阵
谱聚类可以用切割图，随机游走，扰动论等解释

谱聚类算法的重要参数包括：n_clusters, assign_labels, eigen_solver.

这里 n_cluster 表示聚类个数，也表示投影子空间的维数。eigen_solver 表示矩阵分解求特征值的策略，可选取值有 $None, arpack, lobpcg, or\ amg$, 其中， $amg$ 需要安装 $pyamg$ 才能运行，该分解策略能够有效提高大数据集、稀疏问题的计算速度，但可能会导致结果的不稳定。assign_labels 用于在嵌入空间中分配标签的策略。拉普拉斯嵌入后，有两种分配标签的方法。可以应用 kmeans，它是一种流行的选择。但是它也可能对初始化敏感。discretize 是另一种对随机初始化不太敏感的方法。

python 代码示例：

import numpy as np
from sklearn.cluster import SpectralClustering

X = np.array([[1, 1], [2, 1], [1, 0], [4, 7], [3, 5], [3, 6]])
clustering = SpectralClustering(
    n_clusters=2, assign_labels="discretize", random_state=0
).fit(X)
clustering.labels_
# 聚类结果如下
array([1, 1, 1, 0, 0, 0])

也可以直接返回聚类结果，不显示调用 clustering.labels_

SpectralClustering(
    n_clusters=2, assign_labels="discretize", random_state=0
).fit_predict(X)
# 直接打印出来聚类结果
array([1, 1, 1, 0, 0, 0])

层次聚类

层次聚类（Hierarchical clustering）方法对给定的数据集进行层次分解，直到满足某种条件为止。具体地，可分为凝聚式层次聚类和分裂式层次聚类。

凝聚式层次聚类

凝聚式层次聚类又叫作 AGNES 算法。该算法属于层次聚类常采用的算法。相对于下面分裂式层次聚类，该算法复杂度更小。

scikit-learn 中实现的层次聚类算法 AgglomerativeClustering, 使用自底向上执行层次聚类。每个样本都从自己聚类开始，并且聚类被连续合并在一起。合并或链接的标准成为算法的关键点。实现的合并策略的链接标准有 Ward （最小化所有类平方差和，一种方差最小化方法，某种意义上与k -means相似）、Maximum or complete linkage（最小化两对类簇的最大距离）、Average linkage（最小化两对类簇所有观测样本的距离平均值）、Single linkage（最小化两对类簇之间的最小观测样本距离）。不同策略得到的层次聚类效果图如下：

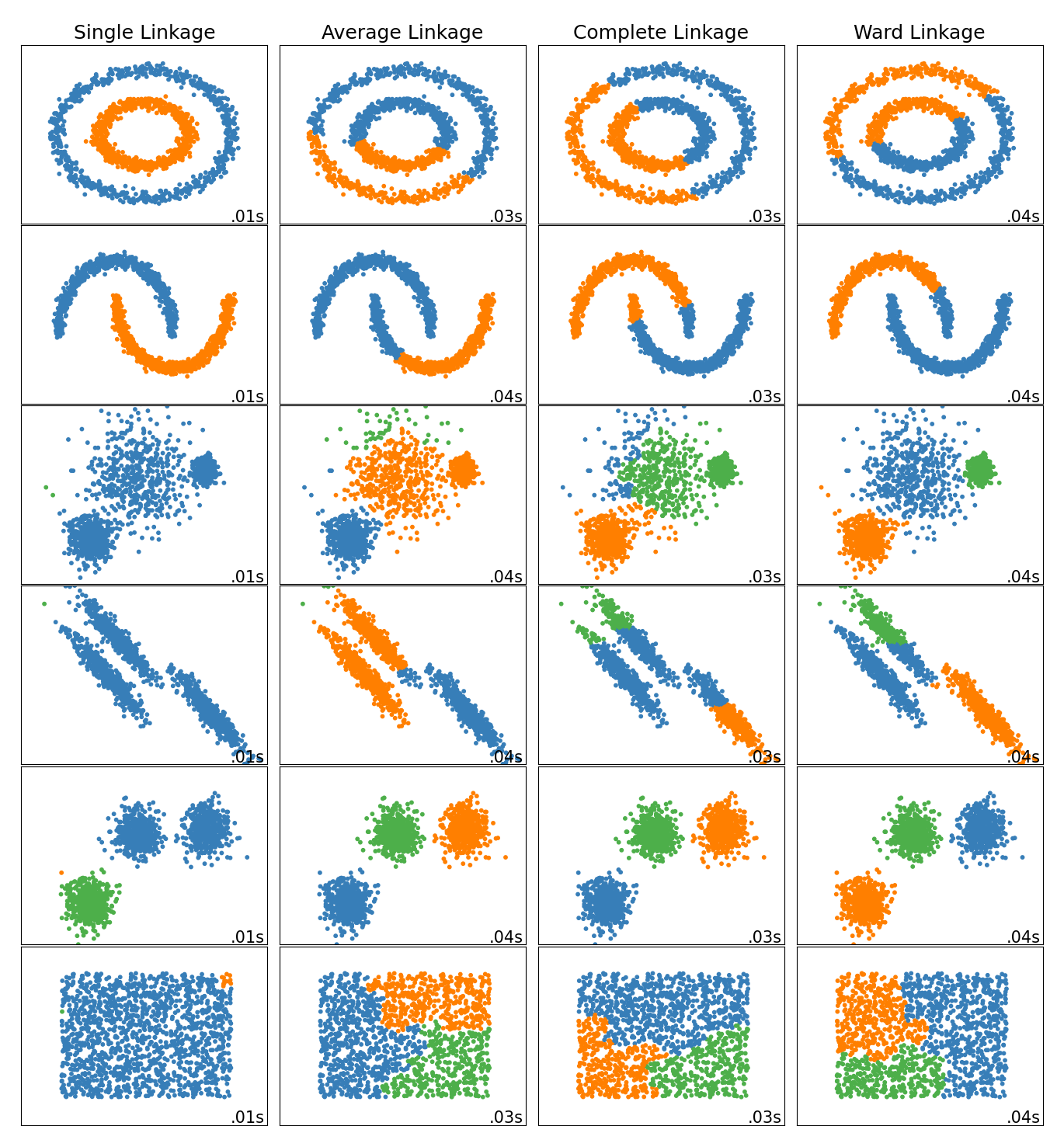
最小距离
- 两个集合中最近的两个样本的聚类，single
- 容易形成链状结构
最大距离
- 两个集合中最远的两个样本的距离，maximum or complete
- 若存在异常值则不稳定
平均距离
- 两个集合中样本间两两距离的平均值，average
- 两个集合中样本间两两距离的平方和，ward

注意，Agglomerative 聚类具有一种 “富人更富有” 的行为，这将导致聚类大小不均匀。在这方面，single linkage 策略是最糟糕的，ward 能够给出最公正的大小。但是，ward 无法更改相似性（或者距离），因此对于非欧度量，average linkage 是一个更好的选择。single linkage 虽然对噪声敏感，但是计算效率高，能够推广到大数据集上。同时，在非球形数据上表现良好。

层次聚类能够给出数据结构的可视化信息，如类似下面的树状图：

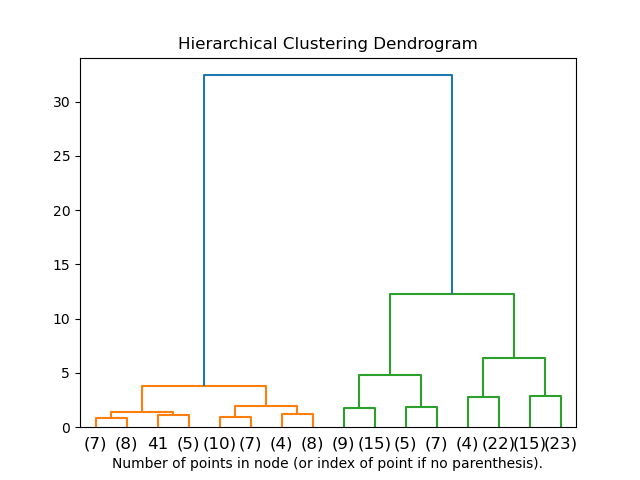
当与连接矩阵一起使用时，AgglomerativeClustering 也可以扩展到大量样本，但是当在样本之间不添加连接限制时，计算开销很大，因为它在每一步都考虑了所有可能的合并。

AgglomerativeClustering 有趣的方面是，可以通过一个连通性矩阵将连通性约束添加到该算法中（只能将相邻的聚类合并在一起），该矩阵为每个样本定义遵循给定数据结构的相邻样本。例如，在下面的瑞士卷示例中，连接性约束禁止合并瑞士卷上不相邻的点，因此避免形成在卷的重叠折叠部分延伸的簇。

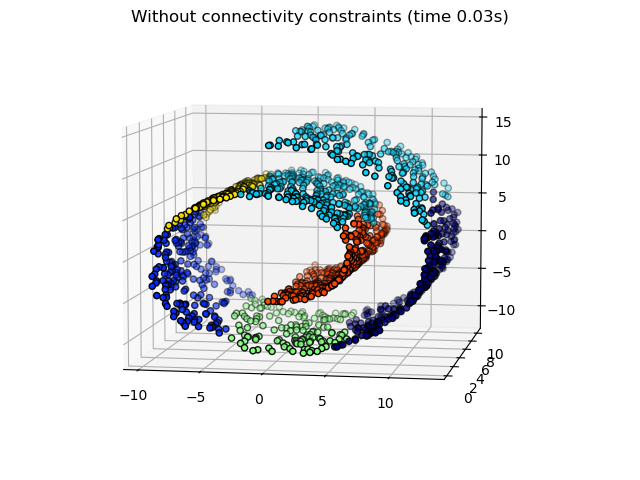
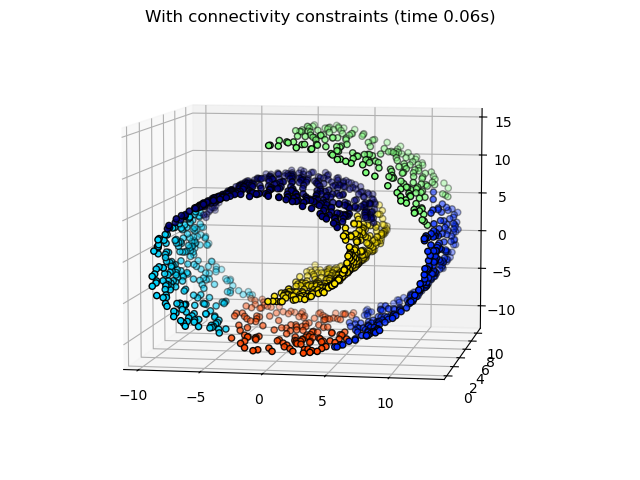
这些约束对于强加特定的局部结构很有用，同时它们也使算法更快，尤其是在样本数量很多时。

层次聚类（这里指 Agglomerative Clustering）的重要参数：n_clusters, linkage.

python 代码示例：

import numpy as np
from sklearn.cluster import AgglomerativeClustering

X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
clustering = AgglomerativeClustering(n_clusters=2, linkage='ward').fit(X)
clustering.labels_
# 运行结果如下
array([1, 1, 1, 0, 0, 0])

# 直接返回聚类结果，不需要调用 clustering.labels_
AgglomerativeClustering(n_clusters=2, linkage='ward').fit_predict(X)
#运行结果如下
array([1, 1, 1, 0, 0, 0])

分裂式层次聚类

分裂式层次聚类是 DIANA 算法。采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。

Birch

Birch 算法叫做平衡迭代削剪聚类算法，它是对层次聚类算法的一种优化，能够处理大数据集。

Birch 使用三元组的聚类特征表示类簇。通过构建满足分支因子和簇直径限制的聚类特征树（Clustering Feature Tree，CFT）来求聚类，数据本质上是有损压缩到一组“群集特征”节点（CF节点）的。聚类特征树其实是一个具有两个参数分支因子和类直径的高度平衡树。分支因子规定了树的每个节点的子女的最多个数，而类直径体现了对这一类点的距离范围。非叶子节点为它的子女的最大特征值。聚类特征树的构建是一个动态过程，可以随时根据数据对模型进行更新操作。

假设一个类簇包含的样本点集合为 ${x_1, x_2, \cdots, x_n}$ ，三元组存储的信息分别是 $(n, s_1, s_2)$，其中 $n$ 表示样本点个数，$s_1 = x_1 + x_2 + \cdots + x_n$，$s_2 = x_1 \cdot x_1 + x_2 \cdot x_2 + \cdots + x_n \cdot x_n$. 根据这个三元组信息，类直径和分支因子可以做如下事情。

类直径：判断样本是否属于当前簇

分支因子：当一个节点的子节点数目超过分支因子的时候，将该节点划分为两个子节点。当一个叶子节点的样本数目超过分支因子的时候，将叶子节点分成两个叶子节点。

优点：

适合大规模数据集，线性效率
节约内存，所有样本都在磁盘上，CFT 仅仅存储 CF 节点和对应的指针
可以识别噪声。还可以对数据集进行初步预处理，作为其他聚类算法的输入，如层次聚类

缺点：

只适合分布呈凸形或者球形的数据集，需要给定聚类个数和簇之间的相关参数
无法很好地缩放到高维数据。根据经验，如果特征维度大于20，通常最好使用 MiniBatchKMeans
由于 CFT 对每个节点的 CF 个数有限制，导致聚类结果可能和真实类别分布不同

Birch 算法的重要参数：threshold, branching_factor, n_clusters.

python 代码示例：

from sklearn.cluster import Birch

X = [[0, 1], [0.3, 1], [-0.3, 1], [0, -1], [0.3, -1], [-0.3, -1]]
brc = Birch(n_clusters=None)
brc.fit(X)
brc.labels_
# 运行结果如下
array([0, 0, 0, 1, 1, 1])

# 直接返回聚类结果，不需要调用 clustering.labels_
brc.fit_predict(X)
#运行结果如下
array([0, 0, 0, 1, 1, 1])

参考链接

OPTICS

OPTICS (Ordering Points To Identify the Clustering Structure) 聚类算法是前面 DBSCAN 算法的一种扩展，能够解决 DBSCAN 对超参数敏感（不易选择超参数）的问题。与 DBSCAN 相比，OPTICS 算法的改进主要在于对输入参数不敏感。

OPTICS 算法不显示地生成数据聚类，它只是对数据对象集合中的对象进行排序，得到一个有序的对象列表，其中包含了足够的信息用来提取聚类。

因为 OPTICS 算法是 DBSCAN 算法的改进，因此很多概念可以沿用，如（直接）密度可达，密度相连，核心点，半径参数 $\varepsilon$，最小点数 $M$ 等。假设数据集 $X = \lbrace x_1, x_2, \cdots, x_n \rbrace$，

核心距离（core distance）

点 $x \in X$ 称为核心点的最小邻域半径定义为 $x$ 的核心距离，
$$
\text{cd} (x) =
\begin{cases}
\text{undefined}, & |N_{\varepsilon}(x)|< M \\
d(x, y(N_{\varepsilon}^M, x)) & |N_{\varepsilon}(x)| \geq M
\end{cases}
$$
其中 $y(N_{\varepsilon}^i, x)$ 表示集合 $N_{\varepsilon}(x)$ 中与点 $x$ 第 $i$ 近邻的点。

从定义可以知道，如果 $x$ 是核心点，那么核心距离 $0 \leq \text{cd}(x) \leq \varepsilon$.

可达距离（reachability distance）

对于点 $x, y \in X$，$y$ 关于 $x$ 的可达距离定义为
$$
\text{rd}(y, x) =
\begin{cases}
\text{undefined}, & |N_{\varepsilon}(x)| < M \\
\max { \text{cd}(x), d(x, y) } & |N_{\varepsilon}(x)| \geq M
\end{cases}
$$
即 $\text{rd}(y, x)$ 表示使得 $x$ 为核心点且 $y$ 从 $x$ 直接密度可达同时成立的最小邻域半径。

通俗理解就是，对于核心点 $x$ ，与点 $x$ 距离小于等于核心距离的可达距离调整为核心距离，大于核心距离的可达距离就是两点之间的距离。

可达距离 $\text{rd}(y, x)$ 的值与点 $y$ 所在空间的密度有关，密度越大，它从相邻节点直接密度可达的距离就越小。如果聚类时想要朝着数据尽量稠密的空间进行扩展，那么可达距离最小的点是最佳的选择。为此，OPTICS 算法中用一个可达距离升序排列的有序种子队列存储带扩展的点，以迅速定位稠密空间的数据对象。

在给出 OPTICS 算法之前，先引入以下定义

$p_i, i = 1, 2, \cdots, N$：OPTICS 算法的输出序数组，$p_i \in \lbrace 1, 2, \cdots, N \rbrace$ 表示排在第 $i$ 个位置的节点的编号
$r_i, i = 1, 2, \cdots, N$：第 $i$ 号节点的可达距离
$c_i, i = 1, 2, \cdots, N$：第 $i$ 号节点的核心距离
$v_i, i = 1, 2, \cdots, N$：表示节点便函是否被访问过的辅助数组，$0$ 表示未访问过，$1$ 表示访问过。这里是否被访问过是指是否被加入到输出序数组 $p$ 中

OPTICS 算法：

初始化
1. 给定参数 $\varepsilon, M$
2. 生成 $N_{\varepsilon}(i), i = 1, 2, \cdots, N$
3. 生成 $c_i, i = 1, 2, \cdots, N$
4. 令 $v_i = 0, i = 1, 2, \cdots, N$
5. 令 $r_i = \text{undefined}, i = 1, 2, \cdots, N$
6. 令 $k = 1, I = \lbrace 1, 2, \cdots, N \rbrace$
7. 将队列 seedlist 初始化为空
主流程

while ($I \neq 0$)

{

从 $I$ 中任取一个元素 $i$，令 $I:= I \ \lbrace i \rbrace$

if ($v_i = 0$) # 表示 $i$ 号节点还没有被处理过

{

（1）令 $v_i = 1$

（2）令 $p_k = i, k = k + 1$

（3）若 $|N_{\varepsilon}(i)| \geq M$ (即 $i$ 为核心点)，则

（3.1）调用 insertlist($N_{\varepsilon}(i), {v_i}{i=1}^N, {r_i}{i=1}^N, c_i$, seedlist)，将 $N_{\varepsilon}(i)$ 中未被访问过的节点按照可达距离插入到队列 seedlist 中。（初始化 seedlist）

（3.2）while (seedlist not empty)

{

（a）从 seedlist 中取出第一个元素 $j$ （其可达距离值最小）

（b）令 $v_j = 1$

（c）令 $p_k = j, k = k + 1$

（d）若 $|N_{\varepsilon}(j)| \geq M$ （即 $j$ 为核心点），则调用 insertlist($N_{\varepsilon}(j), \lbracev_l\rbrace_{l=1}^N, \lbrace_l\rbrace_{l=1}^N, c_j$, seedlist)，将 $N_{\varepsilon}(j)$ 中未被访问过的节点按照可达距离插入到队列 seedlist 中

}

}

}
insertlist($N_{\varepsilon}(j), \lbrace v_l\rbrace_{l=1}^N, \lbrace r_l\rbrace_{l=1}^N, c_j$, seedlist) 模块的算法

for all $J \in N_{\varepsilon}(K)$ do

if ($v_J = 0$)

$\text{rd} = \max \lbrace \text{cd}_K, d(x_K, x_J)\rbrace$

if ($r_J = \text{undefined}$)
1. 令 $r_j = \text{rd}$
2. 将节点 $J$ 按照可达距离值插入到队列 seedlist 的适当位置
  
  else
  
  if ($\text{rd} < r_J$)
  1. 令 $r_J = \text{rd}$
  2. 将节点 $J$ 按照可达距离值插入到队列 seedlist 的适当位置
得到数据 $\lbrace p_i \rbrace_{i=1}^N, \lbrace c_i \rbrace_{i=1}^N, \lbrace r_i \rbrace_{i=1}^N$ 后，就可以利用它们进行聚类。此时还需要一个邻域半径参数 $\lambda \leq \varepsilon$
与 DBSCAN 类似，引入 cluster 标记数组
$$
m_i =
\begin{cases}
j(>0), & x_i 属于第 j 个 \text{cluster} \\
-1, & x_i 为噪声
\end{cases}
$$
所以，要得到一个聚类，只需要生成标记数组 $\lbrace m_i \rbrace_{i=1}^N$ 即可
生成标记数组（ OPTICS Cluster extracting）

clusterID = -1

$k = 1$

for $i = 1, 2, \cdots, N$, do

$j = p_i$

if ($r_j > \lambda$ or $r_j = \text{undefined}$)

if ($c_j \neq \text{undefinded}$ and $c_j \leq \lambda$)

clusterID = $k$

$k = k + 1$

$m_j = $ clusterID

else

$m_j = -1$

else

$m_j = $ clusterID

OPTICS 算法的重要参数：min_samples.

python 代码示例：

import numpy as np
from sklearn.cluster import OPTICS

X = np.array([[1, 2], [2, 5], [3, 6], [8, 7], [8, 8], [7, 3]])
clustering = OPTICS(min_samples=2).fit(X)
clustering.labels_
# 运行结果如下
array([0, 0, 0, 1, 1, 1])

# 直接返回聚类结果，不需要调用 clustering.labels_
OPTICS(min_samples=2).fit_predict(X)
#运行结果如下
array([0, 0, 0, 1, 1, 1])

参考链接

Scikit-learn Clustering

几个聚类算法

K-Means

DBSCAN

谱聚类

层次聚类

凝聚式层次聚类

分裂式层次聚类

Birch

OPTICS

参考链接